Estimation de densité et cartographie¶
Introduction¶
Un maillage hexagonal¶
Un des défauts des représentations par commune tient à l’hétérogénéité de ce maillage en France. La taille des communes diffère énormément, par exemple entre l’Aquitaine ou PACA et le Nord de la France. Cela peut avoir des effets gênants : une commune de grande superficie, même peu peuplée, va avoir un effet visuel fort. Plus embêtant : lorsque le calcul fait intervenir la superficie de la commune, comme dans le cas de la densité de population, on peut obtenir de fortes discontinuités entre communes voisines selon que l’on a une commune de petite taille dont tout le territoire est bâti ou une commune qui a une forêt très étendue sur son territoire (Haguenau, Fontainebleau…) et fait donc apparaître une densité particulièrement faible.
Pour éviter ce défaut, les données sont cartographiées sur un maillage hexagonal qui présente des caractéristiques visuelles plus intéressantes que le carroyage mais qui entraine des calculs plus complexes.
Exemple de maillage hexagonal¶
On peut faire varier la taille des hexagones (pas du maillage) selon la finesse que l’on veut obtenir. Avec un pas de 4 km, on obtient la carte suivante (le fond départemental est ajouté ensuite) :
Estimation de densité¶
Pour calculer la valeur à représenter pour chaque hexagone de ce nouveau maillage, on applique des résultats issus des méthodes d’estimation de densité non paramètrique. L’idée de base de ces techniques est d’estimer, à partir d’un ensemble discret de points de l’espace affectés d’une masse, une fonction continue. La représentation cartographique de cette fonction de densité (plus exactement mesure de Dirac mais on utilisera le terme plus simple de densité) fournit des cartes ayant plusieurs propriétés intéressantes.
Quelques résultats de statistique non paramétrique pour l’estimation de densité¶
Le principe de l’estimation de densité selon une méthode non paramétrique est d’estimer une fonction de densité continue, f(x), à partir d’un échantillon discret X1..Xn supposé issu de cette loi sans faire d’hypothèses a priori sur l’appartenance de f à une famille de lois connues. L’estimation ne concerne donc plus un paramètre dans cette famille de loi, mais directement la fonction elle-même (d’où le terme de non paramétrique).
L’utilisation de la méthode d’estimation par le noyau est la plus fréquente pour estimer une densité. En résumé, on choisit un noyau, c’est-à-dire une fonction, en général continue et de surface 1, ayant de bonnes propriétés de régularité et de symétrie.
Outre le choix d’un noyau, l’estimation de densité nécessite également le choix d’une fenêtre, habituellement notée h.
La statistique non paramétrique donne un certain nombre de résultats et de critères de qualité pour apprécier la qualité de l’estimation de la densité.
Le choix de h a plus d’influence que le choix de K. Parmi les noyaux usuels, l’estimation diffère peu selon que l’on choisisse un noyau gaussien ou un Biweight ; par contre le choix de la fenêtre h est le plus important.
Recette simplifiée pour une carte « biweight »¶
Des données comparables à des effectifs, c’est-à-dire dont la somme a un sens (ex : nombre de vote, population, nombre d’entreprise, solde naturel…) relevés pour un maillage de points qu’on appellera maillage de collecte. Exemple : les communes de France (coordonnées de la mairie), les bureaux de vote, les coordonnées de chaque individu…
Un maillage de représentation, par exemple un maillage hexagonal, qui peut être le même que précédemment mais pas obligatoirement
Un programme qui calcule pour chaque point du maillage de représentation la valeur obtenue à partir des points du maillage de collecte situé dans son voisinage et dépendant de la distance de lissage. En fait le programme fonctionne en « répartissant » sur les différents ipoints du maillage de représentation l’effectif observé pour sur les points du maillage de collecte.
Un outil de représentation cartographique classique puisque l’on dispose d’un fond ce carte (maillage hexagonal) et de valeurs issues du calcul de densité Biweight pour chacun de ces objets.
Exemples de carte¶
Euopéennes 2014¶
Vote FN¶
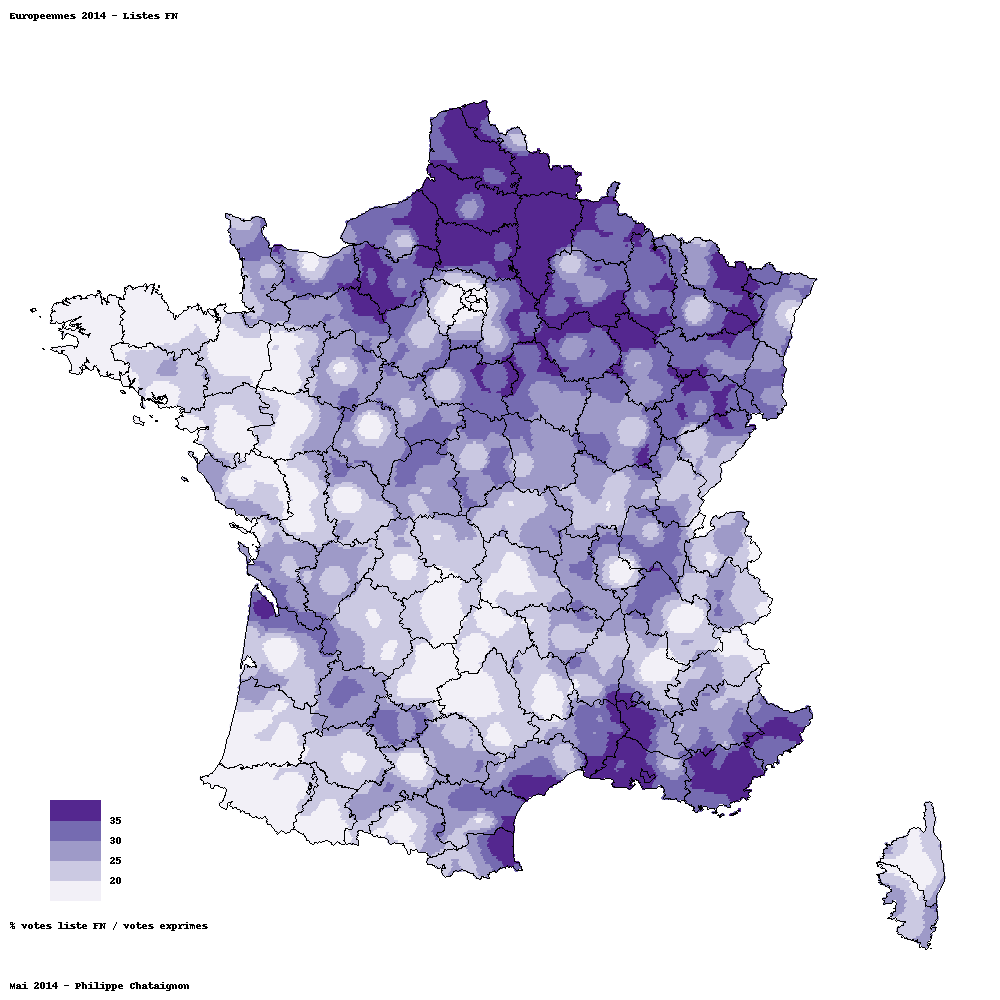
Evolution vote FN¶

Vote UMP¶

Vote union de la gauche¶

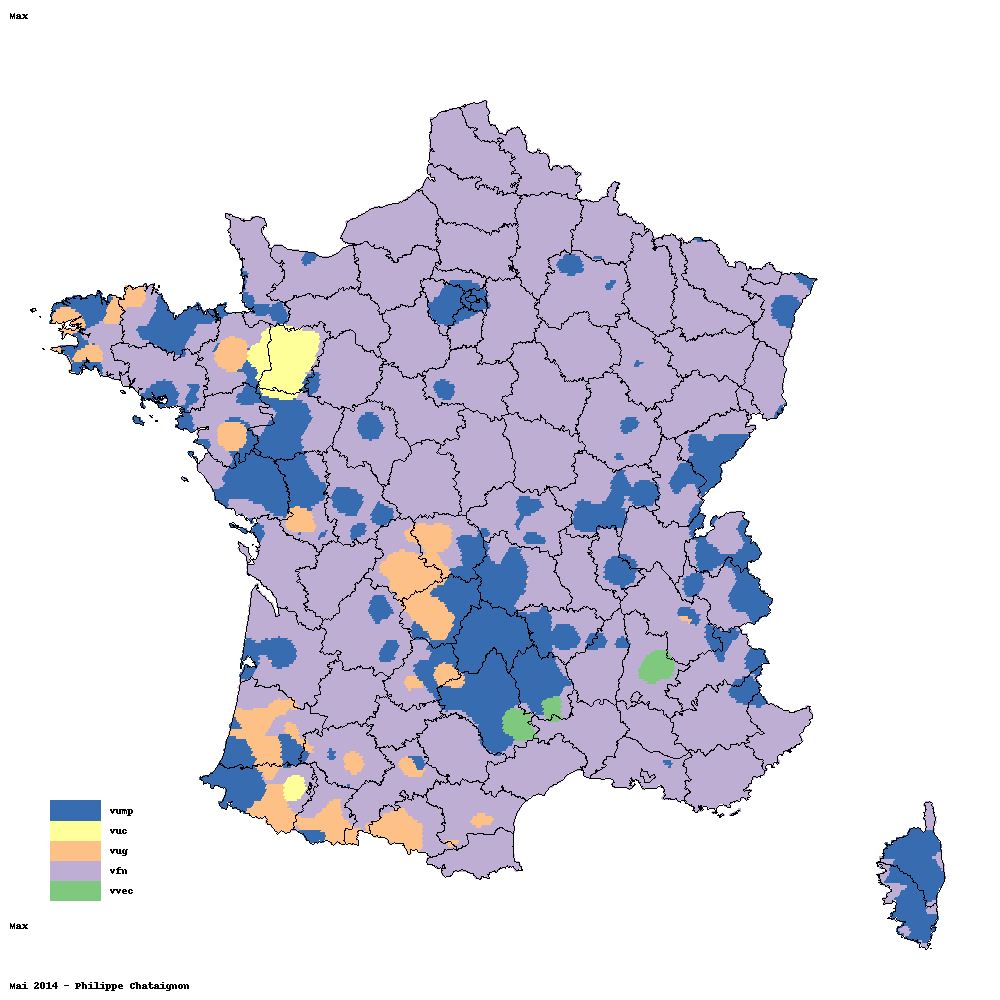
Liste arrivée en tête¶
Population¶
Evolution de population 1999/2011¶
